20th century Dutch physicist Hendrik Lorentz came up with an arbitrary factor, called gamma (\gamma), to make c=c^{\prime} for different IRFs, thereby keeping classical physics equations valid across spacetime. Note that time doesn’t have to be equal in 2 reference frames. It will be denoted in reference frames S and S^{\prime} as t and t^{\prime}.
The gamma factor is defined as \gamma =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}. Note that v is defined as the relative speed between two inertial frames, and c is the speed of light. Using this gamma factors, the following Galilean equations can be used:
x^{\prime}=x-vt becomes x^{\prime}=\gamma(x-vt).
The inverse, x=x^{\prime}+vt is rewritten as x=x^{\prime}+vt^{\prime}, and it becomes x=\gamma(x^{\prime}+vt^{\prime}).
A reminder that the speed of light is the same in each reference frame: c=xt and c^{\prime}=x^{\prime}t^{\prime}.
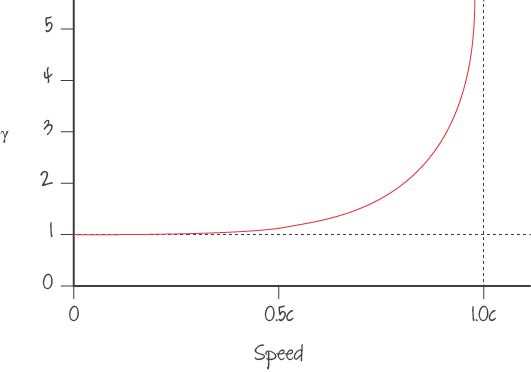
We can see from the graph below that as v approaches 0, the \gamma factor approaches 1, meaning that these equations work in Newtonian mechanics, as \gamma is very close to 1 in regular situations. It is also evident that, as v approaches c, \gamma approaches \infty. From the graph below of \gamma against speed, the speed of light is the asymptote for v, so an accelerated body can never reach c.
Note that the gamma factor has no units, and {\alpha}{\beta}% of c is the same as 0.{\alpha}{\beta}c.

