Both space and time require modification with Lorentz’s gamma factor in order to keep the speed of light invariant. Space modification is known as length contraction, and time modification is known as time dilation.
Instead of being intrinsic physical properties of a moving object, time dilation and length contraction are symmetric properties, being applicable to any objects from two different IRFs. These relational properties are solely the result of coordinate transformations, and thus deal with kinematics, not dynamics.
Time Dilation
Definition: Proper Time is the time interval {\Delta}t_0 measured between two events that take place in the same IRF, at rest to the observer. This definition holds true in any IRF.
When comparing time measurements between IRFs, proper time is always the shortest possible time interval. A moving clock’s time is seen to run slower than that of a stationary clock’s, though this is all relative to an observer. This slowing down of time is time dilation, meaning time extension.
Definition: Dilated time is the time interval {\Delta}t measured for a timepiece in relativistic motion in relation to the observer. Near the speed of light, time slows down.
The equation to calculate for dilated time is: {\Delta}t=\gamma{\Delta}t_0, with the time interval of the stationary clock as {\Delta}t_0, and that of the moving clock as {\Delta}t.
Length Contraction
Definition: Proper Length is the invariant quantity of length measured of an object in the same IRF as the observer. This definition holds true in any IRF.
Proper length is always the longest possible measurement made of an object when comparing reference frame measurements, and is always longer than or equal to a contracted length, meaning shrunken length.
Definition: An entirely relative concept, Contracted Length is the measured length of an object in relativistic motion to the observer. Though this may seem like an optical trick, it is not. The object does not shrink, yet the measured size is real for the observer.
The strangeness of relativity.
The contracted length of an object in relation to its proper length is given by the equation L=\frac{L_0}{\gamma}, where L is the contracted length, and L_0 is the proper length. Note that L_0=v{\Delta}t, where t is the dilated time.
Reality Check
In real life, we do not see time slowing or meter-sticks shrinking to centimetre-sticks simply because we do not go fast enough. Recall that at low speeds \gamma\approx 1, and only as v approaches c does \gamma\to1. This follows that L\to1. Note that length is a 1D concept, so length contraction only occurs along the x-axis.
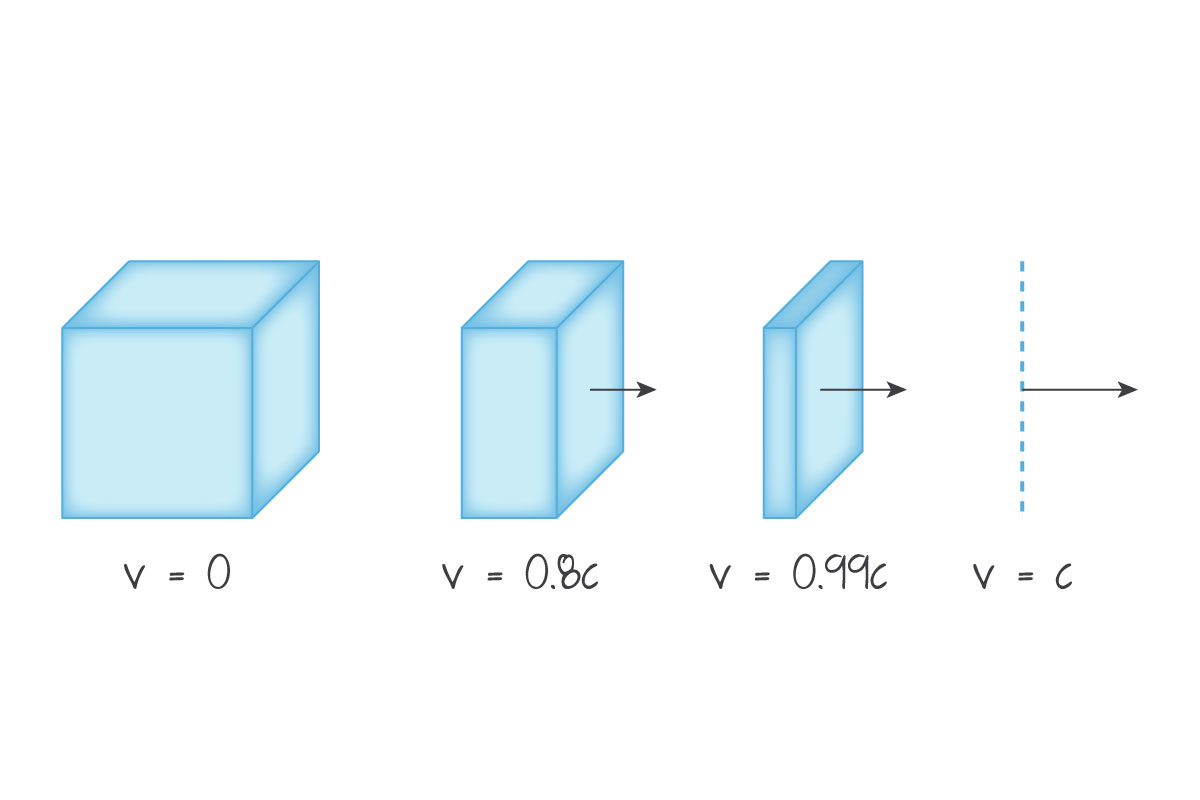
Time and length in physics are all measured values, and measurements cannot be made of moving objects without reference frames. Time dilation and length contraction are real, just objective and quantitative, not subjective.

